Signal Cascade Markov Model

In this example we want to solve a Markovian Masterequation corresponding to a genetic signal cascade. We will use an implicit Euler method in the time direction using the ALS algorithm to solve the individual steps. The construction of the operator will be done according to the SLIM decomposition derived in [P. Gelß et al., 2017] (cf. Example 4.1 therein).

Transition Matrices

Our solution tensor $X[i_1, i_2, \dots]$ represent the likelyhood, that there are $i_1$ copies of protein one, $i_2$ copies of protein two and so on. As the likelyhood of very large $i_j$ becomes small very fast we can restrict ourselves to a finite tensor with $i_j \in \{0,1,\dots,n_j\}$ represented in our sourcecode as

C++Python

const size_t MAX_NUM_PER_SITE = 32;

MAX_NUM_PER_SITE = 32

For the different events we can now describe matrices that have the corresponding action. We will denote as $M$ the creation of a new protein (remove current number of proteins = diagonal equals -1; add current number + 1 proteins = offdiagonal equals 1)

C++Python

Tensor create_M() {
	Tensor M = -1*Tensor::identity({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	for (size_t i = 0; i < MAX_NUM_PER_SITE-1; ++i) {
		M[{i+1, i}] = 1.0;
	}
	return M;
}

def create_M():
	M = -1 * xe.Tensor.identity([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	for i in xrange(MAX_NUM_PER_SITE-1) :
		M[[i+1, i]] = 1.0
	return M

The probability of construction of a protein $x_i$ is actually given in terms of the number of proteins $x_{i-1}$ as $\frac{x_{i-1}}{5+x_{i-1}}$, so we will need another matrix $L$ that gives these probabilities, such that we can later construct the corresponding two-site TT Operator as $L\otimes M$.

C++Python

Tensor create_L() {
	Tensor L({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	L.modify_diagonal_entries([](value_t& _x, const size_t _i) { 
		_x = double(_i)/double(_i+5); 
	});
	return L;
}

def create_L():
	L = xe.Tensor([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	for i in xrange(MAX_NUM_PER_SITE) :
		L[[i,i]] = i / (i+5.0)
	return L

The corresponding destruction could be expressed similarly, but as the probability of destruction in our example only depends on the number of proteins $x_i$ themselves, we will use a matrix denoted as $S$ instead, that already includes these propabilities. Relative to the number of proteins $x_i$ the destruction probability in this example can be given as $0.07 x_i$, we thus have:

C++Python

Tensor create_S() {
	Tensor S({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	
	// Set diagonal
	for (size_t i = 0; i < MAX_NUM_PER_SITE; ++i) {
		S[{i, i}] = -double(i);
	}
	
	// Set offdiagonal
	for (size_t i = 0; i < MAX_NUM_PER_SITE-1; ++i) {
		S[{i, i+1}] = double(i+1);
	}
	return 0.07*S;
}

def create_S():
	S = xe.Tensor([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	
	# set diagonal
	for i in xrange(MAX_NUM_PER_SITE) :
		S[[i,i]] = -i
	
	# set offdiagonal
	for i in xrange(MAX_NUM_PER_SITE-1) :
		S[[i,i+1]] = i+1
	
	return 0.07*S

System Operator

The operator corresponding to the full system of $N$ proteins can now be expressed with the use of these matrices. As can be seen in above mentioned paper, it is given by

$A = \begin{bmatrix} S^* & L & I \end{bmatrix} \otimes \begin{bmatrix} I & 0 & 0 \\ M & 0 & 0 \\ S & L & I \end{bmatrix} \otimes \cdots \otimes \begin{bmatrix} I & 0 & 0 \\ M & 0 & 0 \\ S & L & I \end{bmatrix} \otimes \begin{bmatrix} I \\ M \\ S \end{bmatrix}$

where $S^*$ includes the construction of the first protein (that does not depend on any other proteins) as $S^* = 0.7\cdot M + S$.

The construction of this operator in xerus is straight-forward: we first construct the individual matrices, use them to construct the components as given in the previous formula and then simply set them via .set_component as the components of our operator.

C++Python

TTOperator create_operator(const size_t _degree) { 
	const Index i, j, k, l;
	
	// Create matrices
	const Tensor M = create_M();
	const Tensor S = create_S();
	const Tensor L = create_L();
	const Tensor Sstar = 0.7*M + S;
	const Tensor I = Tensor::identity({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	
	// Create empty TTOperator
	TTOperator A(2*_degree);
	
	// Create first component
	Tensor comp;
	comp(i, j, k, l) = 
		Sstar(j, k) * Tensor::dirac({1, 3}, 0)(i, l) 
		+   L(j, k) * Tensor::dirac({1, 3}, 1)(i, l) 
		+   I(j, k) * Tensor::dirac({1, 3}, 2)(i, l);
    
	A.set_component(0, comp); 
	
	// Create middle components
	comp(i, j, k, l) =
		  I(j, k) * Tensor::dirac({3, 3}, {0, 0})(i, l)
		+ M(j, k) * Tensor::dirac({3, 3}, {1, 0})(i, l)
		+ S(j, k) * Tensor::dirac({3, 3}, {2, 0})(i, l)
		+ L(j, k) * Tensor::dirac({3, 3}, {2, 1})(i, l)
		+ I(j, k) * Tensor::dirac({3, 3}, {2, 2})(i, l);
	
	for(size_t c = 1; c+1 < _degree; ++c) {
		A.set_component(c, comp);
	}
	
	// Create last component
	comp(i, j, k, l) = 
		  I(j, k) * Tensor::dirac({3, 1}, 0)(i, l) 
		+ M(j, k) * Tensor::dirac({3, 1}, 1)(i, l) 
		+ S(j, k) * Tensor::dirac({3, 1}, 2)(i, l);
    
	A.set_component(_degree-1, comp);
	
	return A;
}

def create_operator(degree):
	i,j,k,l = xe.indices(4)
	
	# create matrices
	M = create_M()
	S = create_S()
	L = create_L()
	Sstar = 0.7*M + S;
	I = xe.Tensor.identity([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	
	# create empty TTOperator
	A = xe.TTOperator(2*degree)
	
	# create first component
	comp = xe.Tensor()
	comp(i, j, k, l) << \
		Sstar(j, k) * xe.Tensor.dirac([1, 3], 0)(i, l) \
		+   L(j, k) * xe.Tensor.dirac([1, 3], 1)(i, l) \
		+   I(j, k) * xe.Tensor.dirac([1, 3], 2)(i, l)
	
	A.set_component(0, comp)
	
	# create middle components
	comp(i, j, k, l) << \
		  I(j, k) * xe.Tensor.dirac([3, 3], [0, 0])(i, l) \
		+ M(j, k) * xe.Tensor.dirac([3, 3], [1, 0])(i, l) \
		+ S(j, k) * xe.Tensor.dirac([3, 3], [2, 0])(i, l) \
		+ L(j, k) * xe.Tensor.dirac([3, 3], [2, 1])(i, l) \
		+ I(j, k) * xe.Tensor.dirac([3, 3], [2, 2])(i, l)
	
	for c in xrange(1, degree-1) :
		A.set_component(c, comp)
	
	# create last component
	comp(i, j, k, l) << \
		  I(j, k) * xe.Tensor.dirac([3, 1], 0)(i, l) \
		+ M(j, k) * xe.Tensor.dirac([3, 1], 1)(i, l) \
		+ S(j, k) * xe.Tensor.dirac([3, 1], 2)(i, l)
	
	A.set_component(degree-1, comp)
	
	return A

Implicit Euler

To solve the Masterequation in the time domain we will use a simple implicit Euler method. In every step we have to solve $ (I-\tau A) x_{i+1} = x_i $ for $x_{i+1}$. To do so, we will use the xerus builtin ALS method. From previous experiments we know, that the _SPD (for “symmetric positive semi-definite”) variant of the ALS works fine in this setting even though the operator is not symmetric. To define the parameters only once, we create our own ALS variation.

We will keep an eye on the residual after each step for the purpose of this example to ensure, that these claims actually hold true, and will store the result of every step to be able to plot the mean concentrations over time in the end.

To ensure, that the entries of the solution tensor actually represent probabilities we will also normalize the tensor at every step to ensure that its one-norm is equal to 1. This norm is usually hard to calculate, but under the assumption that all entries are positive we can express it as a simple contraction with a ones-tensor.

C++Python

double one_norm(const TTTensor &_x) {
	Index j;
	return double(_x(j&0) * TTTensor::ones(_x.dimensions)(j&0));
}

std::vector<TTTensor> implicit_euler(const TTOperator& _A, TTTensor _x, 
			const double _stepSize, const size_t _n) 
{ 
	const TTOperator op = TTOperator::identity(_A.dimensions)-_stepSize*_A;
	
	Index j,k;
	auto ourALS = ALS_SPD;
	ourALS.convergenceEpsilon = 1e-4;
	ourALS.numHalfSweeps = 100;
	
	std::vector<TTTensor> results;
	TTTensor nextX = _x;
	results.push_back(_x);
    
	for(size_t i = 0; i < _n; ++i) {
		ourALS(op, nextX, _x);
        
		// Normalize
		double norm = one_norm(nextX);
		nextX /= norm;
		
		XERUS_LOG(iter, "Done itr " << i 
				<< " residual: " << frob_norm(op(j/2,k/2)*nextX(k&0) - _x(j&0)) 
				<< " one-norm: " << norm);
		
		_x = nextX;
		results.push_back(_x);
	}
	
	return results;
}

def one_norm(x):
	i = xe.Index()
	return float(x(i&0) * xe.TTTensor.ones(x.dimensions)(i&0))

def implicit_euler(A, x, stepSize, n):
	op = xe.TTOperator.identity(A.dimensions) - stepSize*A
	
	j,k = xe.indices(2)
	ourALS = xe.ALS_SPD
	ourALS.convergenceEpsilon = 1e-4
	ourALS.numHalfSweeps = 100
	
	results = [x]
	nextX = xe.TTTensor(x)
	
	for i in xrange(n) :
		ourALS(op, nextX, x)
		
		# normalize
		norm = one_norm(nextX)
		nextX /= norm
		
		print("done itr", i, \
			"residual:", xe.frob_norm(op(j/2,k/2)*nextX(k&0) - x(j&0)), \
			"one-norm:", norm)
		
		x = xe.TTTensor(nextX) # ensure it is a copy
		results.append(x)
	
	return results

All we have to do now, is to provide a starting point (no proteins with probability 1) and call the appropriate functions. As our implicit Euler method as it stands has no means of adapting the rank of the solution we will increaseit from the start by adding a small pertubation to the starting configuration. To do this we have to convert the (sparse) dirac TTTensor to dense representation because sparse TT cannot (yet) be added to other TTTensors (see the TTTensor documentation).

C++Python

int main() {
	const size_t numProteins = 10;
	const size_t numSteps = 200;
	const double stepSize = 1.0;
	const size_t rankX = 3;
	
	const auto A = create_operator(numProteins);
	
	auto start = TTTensor::dirac(
			std::vector<size_t>(numProteins, MAX_NUM_PER_SITE), 
			0
	);
	start.use_dense_representations();
	start += 1e-14 * TTTensor::random(
			start.dimensions, 
			std::vector<size_t>(start.degree()-1, rankX-1)
	);
	
	const auto results = implicit_euler(A, start, stepSize, numSteps);
}

numProteins = 10
numSteps = 200
stepSize = 1.0
rankX = 3

A = create_operator(numProteins)

start = xe.TTTensor.dirac([MAX_NUM_PER_SITE]*numProteins, 0)
start.use_dense_representations()
start += 1e-14 * xe.TTTensor.random( \
		start.dimensions, \
		[rankX-1]*(start.degree()-1))

results = implicit_euler(A, start, stepSize, numSteps)

Output

At this point we have calculated the solution tensors and can start ot calculate quantities of interest from them. For the purpose of this example we will simple calculate the mean concentration of every protein at every timestep. To calculate the mean we simply have to weight the mode corresponding to the protein in question with the number of proteins it represents (the vector $(0, 1, 2, \dots)$) and sum over all other protein configurations (ie. contract a ones-vector to those modes). We will use the most general TensorNetwork class to write these contractions. This way xerus can be very lazy and only perform any actions (and decide upon a contraction order) when we query it for the final value.

C++Python

double get_mean_concentration(const TTTensor& _res, const size_t _i) { 
	const Index k,l;
	TensorNetwork result(_res);
	const Tensor weights({MAX_NUM_PER_SITE}, [](const size_t _k){ 
		return double(_k); 
	});
	const Tensor ones = Tensor::ones({MAX_NUM_PER_SITE});
	
	for (size_t j = 0; j < _res.degree(); ++j) {
		if (j == _i) {
			result(l&0) = result(k, l&1) * weights(k);
		} else {
			result(l&0) = result(k, l&1) * ones(k);
		}
	}
	// at this point the degree of 'result' is 0, so there is only one entry
	return result[{}]; 
}

def get_mean_concentration(x, i):
	k,l = xe.indices(2)
	result = xe.TensorNetwork(x)
	weights = xe.Tensor.from_function([MAX_NUM_PER_SITE], lambda idx: idx[0])
	ones = xe.Tensor.ones([MAX_NUM_PER_SITE])
	
	for j in xrange(x.degree()) :
		if j == i :
			result(l&0) << result(k, l&1) * weights(k)
		else :
			result(l&0) << result(k, l&1) * ones(k)
	
	# at this point the degree of 'result' is 0, so there is only one entry
	return result[[]]

Observing the evolution of concentrations over time is now a simple matter of iterating over all solution steps and proteins.

C++Python

void print_mean_concentrations_to_file(const std::vector<TTTensor> &_result) {
	std::fstream out("mean.dat", std::fstream::out);
	for (const auto& res : _result) {
		for (size_t k = 0; k < res.degree(); ++k) {
			out << get_mean_concentration(res, k) << ' ';
		}
		out << std::endl;
	}
}

def print_mean_concentrations_to_file(results):
	f = open("mean.dat", 'w')
	for res in results :
		for k in xrange(res.degree()) :
			f.write(str(get_mean_concentration(res, k))+' ')
		f.write('\n')
	f.close()

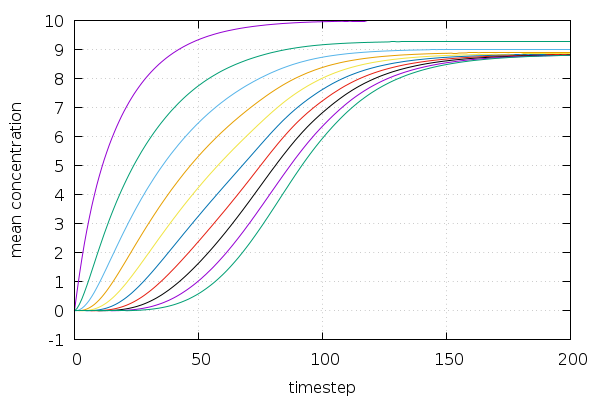
The solution shows nice saturation curves for all individual proteins:

Ten saturation curves with different onsets.

Complete Sourcecode

The full source code of this example looks as follows

C++Python

#include <xerus.h>
#include <iostream>
#include <string>
#include <fstream>

using namespace xerus;

const size_t MAX_NUM_PER_SITE = 32;

Tensor create_M() {
	Tensor M = -1*Tensor::identity({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	for (size_t i = 0; i < MAX_NUM_PER_SITE-1; ++i) {
		M[{i+1, i}] = 1.0;
	}
	return M;
}

Tensor create_L() {
	Tensor L({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	L.modify_diagonal_entries([](value_t& _x, const size_t _i) { 
		_x = double(_i)/double(_i+5); 
	});
	return L;
}

Tensor create_S() {
	Tensor S({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	
	// Set diagonal
	for (size_t i = 0; i < MAX_NUM_PER_SITE; ++i) {
		S[{i, i}] = -double(i);
	}
	
	// Set offdiagonal
	for (size_t i = 0; i < MAX_NUM_PER_SITE-1; ++i) {
		S[{i, i+1}] = double(i+1);
	}
	return 0.07*S;
}



TTOperator create_operator(const size_t _degree) { 
	const Index i, j, k, l;
	
	// Create matrices
	const Tensor M = create_M();
	const Tensor S = create_S();
	const Tensor L = create_L();
	const Tensor Sstar = 0.7*M+S;
	const Tensor I = Tensor::identity({MAX_NUM_PER_SITE, MAX_NUM_PER_SITE});
	
	// Create empty TTOperator
	TTOperator A(2*_degree);
	
	Tensor comp;
	
	// Create first component
	comp(i, j, k, l) = 
		Sstar(j, k)*Tensor::dirac({1, 3}, 0)(i, l) 
		+   L(j, k)*Tensor::dirac({1, 3}, 1)(i, l) 
		+   I(j, k)*Tensor::dirac({1, 3}, 2)(i, l);
    
	A.set_component(0, comp); 
	
	// Create middle components
	comp(i, j, k, l) =
		  I(j, k) * Tensor::dirac({3, 3}, {0, 0})(i, l)
		+ M(j, k) * Tensor::dirac({3, 3}, {1, 0})(i, l)
		+ S(j, k) * Tensor::dirac({3, 3}, {2, 0})(i, l)
		+ L(j, k) * Tensor::dirac({3, 3}, {2, 1})(i, l)
		+ I(j, k) * Tensor::dirac({3, 3}, {2, 2})(i, l);
	
	for(size_t c = 1; c+1 < _degree; ++c) {
		A.set_component(c, comp);
	}
	
	// Create last component
	comp(i, j, k, l) = 
		  I(j, k)*Tensor::dirac({3, 1}, 0)(i, l) 
		+ M(j, k)*Tensor::dirac({3, 1}, 1)(i, l) 
		+ S(j, k)*Tensor::dirac({3, 1}, 2)(i, l);
    
	A.set_component(_degree-1, comp);
	
	return A;
}

/// @brief calculates the one-norm of a TTTensor, assuming that all entries in it are positive
double one_norm(const TTTensor &_x) {
	Index j;
	return double(_x(j&0) * TTTensor::ones(_x.dimensions)(j&0));
}

std::vector<TTTensor> implicit_euler(const TTOperator& _A, TTTensor _x, 
			const double _stepSize, const size_t _n) 
{ 
	const TTOperator op = TTOperator::identity(_A.dimensions)-_stepSize*_A;
	
	Index j,k;
	auto ourALS = ALS_SPD;
	ourALS.convergenceEpsilon = 0;
	ourALS.numHalfSweeps = 2;
	
	std::vector<TTTensor> results;
	TTTensor nextX = _x;
	results.push_back(_x);
    
	for(size_t i = 0; i < _n; ++i) {
		ourALS(op, nextX, _x);
        
		// Normalize
		double norm = one_norm(nextX);
		nextX /= norm;
		
		XERUS_LOG(iter, "Done itr " << i 
				<< " residual: " << frob_norm(op(j/2,k/2)*nextX(k&0) - _x(j&0)) 
				<< " norm: " << norm);
		
		_x = nextX;
		results.push_back(_x);
	}
	
	return results;
}

double get_mean_concentration(const TTTensor& _res, const size_t _i) { 
	const Index k,l;
	TensorNetwork result(_res);
		const Tensor weights({MAX_NUM_PER_SITE}, [](const size_t _k){ 
		return double(_k); 
	});
	const Tensor ones = Tensor::ones({MAX_NUM_PER_SITE});
	
	for (size_t j = 0; j < _res.degree(); ++j) {
		if (j == _i) {
			result(l&0) = result(k, l&1) * weights(k);
		} else {
			result(l&0) = result(k, l&1) * ones(k);
		}
	}
	// at this point the degree of 'result' is 0, so there is only one entry
	return result[{}]; 
}

void print_mean_concentrations_to_file(const std::vector<TTTensor> &_result) {
	std::fstream out("mean.dat", std::fstream::out);
	for (const auto& res : _result) {
		for (size_t k = 0; k < res.degree(); ++k) {
			out << get_mean_concentration(res, k) << ' ';
		}
		out << std::endl;
	}
}

int main() {
	const size_t numProteins = 10;
	const size_t numSteps = 300;
	const double stepSize = 1.0;
	const size_t rankX = 3;
	
	auto start = TTTensor::dirac(
			std::vector<size_t>(numProteins, MAX_NUM_PER_SITE), 
			0
	);
	start.use_dense_representations();
	start += 1e-14 * TTTensor::random(
			start.dimensions, 
			std::vector<size_t>(start.degree()-1, rankX-1)
	);
	const auto A = create_operator(numProteins);
	
	const auto results = implicit_euler(A, start, stepSize, numSteps);
	
	print_mean_concentrations_to_file(results);
}

import xerus as xe

MAX_NUM_PER_SITE = 32

def create_M():
	M = -1 * xe.Tensor.identity([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	for i in xrange(MAX_NUM_PER_SITE-1) :
		M[[i+1, i]] = 1.0
	return M

def create_L():
	L = xe.Tensor([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	for i in xrange(MAX_NUM_PER_SITE) :
		L[[i,i]] = i / (i+5.0)
	return L

def create_S():
	S = xe.Tensor([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	
	# set diagonal
	for i in xrange(MAX_NUM_PER_SITE) :
		S[[i,i]] = -i
	
	# set offdiagonal
	for i in xrange(MAX_NUM_PER_SITE-1) :
		S[[i,i+1]] = i+1
	
	return 0.07*S


def create_operator(degree):
	i,j,k,l = xe.indices(4)
	
	# create matrices
	M = create_M()
	S = create_S()
	L = create_L()
	Sstar = 0.7*M + S;
	I = xe.Tensor.identity([MAX_NUM_PER_SITE, MAX_NUM_PER_SITE])
	
	# create empty TTOperator
	A = xe.TTOperator(2*degree)
	
	# create first component
	comp = xe.Tensor()
	comp(i, j, k, l) << \
		Sstar(j, k) * xe.Tensor.dirac([1, 3], 0)(i, l) \
		+   L(j, k) * xe.Tensor.dirac([1, 3], 1)(i, l) \
		+   I(j, k) * xe.Tensor.dirac([1, 3], 2)(i, l)
	
	A.set_component(0, comp)
	
	# create middle components
	comp(i, j, k, l) << \
		  I(j, k) * xe.Tensor.dirac([3, 3], [0, 0])(i, l) \
		+ M(j, k) * xe.Tensor.dirac([3, 3], [1, 0])(i, l) \
		+ S(j, k) * xe.Tensor.dirac([3, 3], [2, 0])(i, l) \
		+ L(j, k) * xe.Tensor.dirac([3, 3], [2, 1])(i, l) \
		+ I(j, k) * xe.Tensor.dirac([3, 3], [2, 2])(i, l)
	
	for c in xrange(1, degree-1) :
		A.set_component(c, comp)
	
	# create last component
	comp(i, j, k, l) << \
		  I(j, k) * xe.Tensor.dirac([3, 1], 0)(i, l) \
		+ M(j, k) * xe.Tensor.dirac([3, 1], 1)(i, l) \
		+ S(j, k) * xe.Tensor.dirac([3, 1], 2)(i, l)
	
	A.set_component(degree-1, comp)
	
	return A


def one_norm(x):
	i = xe.Index()
	return float(x(i&0) * xe.TTTensor.ones(x.dimensions)(i&0))

def implicit_euler(A, x, stepSize, n):
	op = xe.TTOperator.identity(A.dimensions) - stepSize*A
	
	j,k = xe.indices(2)
	ourALS = xe.ALS_SPD
	ourALS.convergenceEpsilon = 1e-4
	ourALS.numHalfSweeps = 100
	
	results = [x]
	nextX = xe.TTTensor(x)
	
	for i in xrange(n) :
		ourALS(op, nextX, x)
		
		# normalize
		norm = one_norm(nextX)
		nextX /= norm
		
		print("done itr", i, \
			"residual:", xe.frob_norm(op(j/2,k/2)*nextX(k&0) - x(j&0)), \
			"one-norm:", norm)
		
		x = xe.TTTensor(nextX) # ensure it is a copy
		results.append(x)
	
	return results


def get_mean_concentration(x, i):
	k,l = xe.indices(2)
	result = xe.TensorNetwork(x)
	weights = xe.Tensor.from_function([MAX_NUM_PER_SITE], lambda idx: idx[0])
	ones = xe.Tensor.ones([MAX_NUM_PER_SITE])
	
	for j in xrange(x.degree()) :
		if j == i :
			result(l&0) << result(k, l&1) * weights(k)
		else :
			result(l&0) << result(k, l&1) * ones(k)
	
	# at this point the degree of 'result' is 0, so there is only one entry
	return result[[]]

def print_mean_concentrations_to_file(results):
	f = open("mean.dat", 'w')
	for res in results :
		for k in xrange(res.degree()) :
			f.write(str(get_mean_concentration(res, k))+' ')
		f.write('\n')
	f.close()


numProteins = 10
numSteps = 200
stepSize = 1.0
rankX = 3

A = create_operator(numProteins)

start = xe.TTTensor.dirac([MAX_NUM_PER_SITE]*numProteins, 0)
for i in xrange(numProteins) :
	start.set_component(i, start.get_component(i).dense_copy())

start += 1e-14 * xe.TTTensor.random(start.dimensions, [rankX-1]*(start.degree()-1))

results = implicit_euler(A, start, stepSize, numSteps)

print_mean_concentrations_to_file(results)

Examples

Signal Cascade Markov Model

Transition Matrices

System Operator

Implicit Euler

Output

Complete Sourcecode

Examples